Aristóteles, (Estagira, Macedonia 384 a. C. – Calcis Eubea, Grecia 322 a. C.), es uno de los más grandes filósofos de la antigüedad y acaso de la historia de la filosofía occidental. Fue creador de la lógica, precursor de la anatomía y la biología y un creador de la taxonomía. Está considerado Aristóteles (junto a Platón) como el determinante de gran parte del corpum de creencias centrales del Pensamiento Occidental como del hombre corriente (aquello que hoy denominamos "sentido común" del hombre occidental), pruebas de ello son la Lógica y el principio de "no contradicción", hoy sabemos que Aristóteles inaguró toda una nueva visión del mundo.
El punto de partida fue Platón, pero pronto adoptó una actitud crítica frente a éste. No dejó de lado las enseñanzas de Platón, sino que «ató los cabos sueltos» y desarrolló las ideas de su antiguo maestro.
La influencia que Aristóteles ha tenido en el mundo es extraordinaria. Toda la antigüedad se hace cargo o dueña de su ingente enciclopedia. Su Metafísica será el basamento filosófico de la posteridad.
Fueron los árabes los que redescubrieron a Aristóteles y a través de ellos pasó a la filosofía escolástica.
En el Renacimiento su filosofía se ve opacada por un eclipse histórico momentáneo. Los nuevos conceptos científicos lo llevan a un segundo plano. Pero su influjo, aunque ya no en la física, seguirá vigente en el pensamiento filosófico en sentido estricto en todos los grandes pensadores, en Leibniz, en Hegel, etc.
Nada es más formador como desentrañar el sentido de sus textos, a veces abstrusos, pero siempre profundos, abarcadores e ilustrativos.
http://es.wikipedia.org/wiki/Aristóteles
Arquímedes (Siracusa, Sicilia, 287 - 212 a.c.), matemático y geómetro griego, considerado el más notable científico y matemático de la antigüedad, es recordado por el Principio de Arquímedes y por sus aportes a la cuadratura del círculo, el estudio de la palanca, el tornillo de Arquímedes, la espiral de Arquímedes y otros aportes a la matemática, la ingeniería y la geometría.
Hijo del astrónomo Fidias, quien probablemente le introdujo en las matemáticas, Arquímedes estudió en Alejandría, donde tuvo como maestro a Conón de Samos y entró en contacto con Eratóstenes; a este último dedicó Arquímedes su Método.
Aunque probablemente su contribución científica más conocida sea el principio de la hidrostática que lleva su nombre, el Principio de Arquímedes, no fueron menos notables sus disquisiciones acerca de la cuadratura del círculo, el descubrimiento de la relación aproximada entre la circunferencia y su diámetro, relación que se designa hoy día con la letra griega π (pi).
Arquímedes demostró que el lado del hexágono regular inscrito en un círculo es igual al radio de dicho círculo, así como que el lado del cuadrado circunscrito a un círculo es igual al diámetro de dicho círculo. De la primera proposición dedujo que el perímetro del hexágono inscrito era 3 veces el diámetro de la circunferencia, mientras que de la segunda dedujo que el perímetro del cuadrado circunscrito era 4 veces el diámetro de la circunferencia.
Afirmó, además, que toda línea cerrada envuelta por otra es de menor longitud que ésta, por lo que la circunferencia debía ser mayor que tres diámetros pero menor que cuatro. Por medio de sucesivas inscripciones y circunscripciones de polígonos regulares llegó a determinar el valor aproximado de π como:
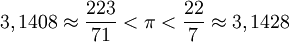
Con los rudimentarios medios de los que disponía el sabio griego, el error absoluto que cometió en el cálculo de π resultó ser inferior a una milésima (0,0040 %).
Sin embargo, Arquímedes es más conocido por enunciar el principio que lleva su nombre:
- Principio de Arquímedes: todo cuerpo sumergido en un fluido experimenta un empuje vertical y hacia arriba igual al peso de fluido desalojado.
Inventó una máquina para la elevación de agua, el
tornillo de Arquímedes, así como la
balanza que lleva su nombre; enunció la
ley de la palanca lo que le llevó a proferir la célebre frase
Dadme un punto de apoyo y moveré el mundo; inventó la polea compuesta, basada en el principio de la palanca
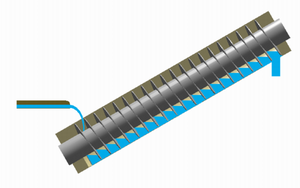
Tornillo de Arquímedes.
http://es.wikipedia.org/wiki/ArquÃÂmedes
El nombre de Hipatia significa la más grande. La leyenda de Hipatia de Alejandría nos muestra a una joven, virgen y bella, matemática y filósofa, cuya muerte violenta marca un punto de inflexión entre la cultura del razonamiento griego y el oscurantismo del mundo medieval. Como ocurre con todas las biografías de los matemáticos (y matemáticas) de la antigüedad, se sabe muy poco de su vida, y de su obra se conoce sólo una pequeña parte.
Fue recordada como una gran maestra y admirada por la magnitud de sus conocimientos. Era considerada como el mejor matemático vivo del mundo greco-romano. En la época de la Ilustración, Toland y Voltaire, utilizaron su figura como expresión de la irracionalidad del fanatismo religioso, y en el Romanticismo la recrearon como la encarnación del espíritu de Platón y el cuerpo de Afrodita. Pero toda esta notoriedad ha hecho que se pierdan de vista sus logros intelectuales y su auténtica biografía. Enseñó Matemáticas, Astronomía y Filosofía, escribió un trabajo titulado “El Canón Astronómico”, comentó las grandes obras de la matemática griega como la “Aritmética” de Diofanto, “Las Cónicas” de Apolonio, el libro III del “Almagesto” de Tolomeo, probablemente comentara junto a su padre, los “Elementos” de Euclides y el resto del “Almagesto”. Construyó instrumentos científicos como el astrolabio y el hidroscopio.
http://divulgamat.ehu.es/weborriak/historia/MateOspetsuak/Hipatia.asp
Pitágoras, nació en la isla de Samos en el año 582 a. C. Siendo muy joven viajó a Mesopotamia y Egipto. Se estableció en la Magna Grecia, en Crotona alrededor del 525 a.C., en el sur de Italia,donde fundó su segunda escuela. Las doctrinas de este centro culturaleran regidas por reglas muy estrictas de conducta. Su escuela (aunquerigurosamente esotérica) estaba abierta a hombres y mujeresindistintamente, y la conducta discriminatoria estaba prohibida(excepto impartir conocimiento a los no iniciados). Sus estudiantespertenecían a todas las razas, religiones, y estratos económicos ysociales. Tras ser expulsados por los pobladores de Crotona, lospitagóricos se exiliaron en Tarento donde se fundó su tercera escuela.A su escuela de pensamiento se la conocía como los pitagóricos y afirmaban que la estructura del universo era aritmética y geométrica.Políticamente apoyaron el partido dórico, obteniendo grandes cuotas depoder hasta el Siglo V, en el que fueron perseguidos y donde muchos desus miembros murieron. La hermandad estaba dividida en dos partes: Losestudiantes y los oyentes. Los estudiantes aprendían las enseñanzasmatemáticas, religiosas y filosóficas directamente de su fundador,mientras que los oyentes se limitaban a ver el modo de comportarse delos pitagóricos .
Los pitagóricos atribuían todos sus descubrimientos a Pitágoras porlo que es difícil determinar con exactitud cuales resultados son obradel maestro y cuales de los discípulos.
Los números pentagonales son un ejemplo de números figurados.
Entre los descubrimientos que se atribuyen a la escuela de Pitágoras están:[2]
- Una prueba del teorema de Pitágoras.Si bien los pitagóricos no descubrieron este teorema (ya era conocido yaplicado en Babilonia y la India desde hacía un tiempo considerable),sí fueron los primeros en encontrar una demostración formal delteorema. También demostraron el converso del teorema (si los lados deun triángulo satisfacen la ecuación, entonces el triángulo es recto).
- Ternas pitagóricas. Una terna pitagórica es una terna de números enteros (a, b, c) tales que a²+b²=c².Aunque los babilonios ya sabían cómo generar tales ternas en ciertoscasos, los pitagóricos extendieron el estudio del tema encontrandoresultados como cualquier entero impar es miembro de una terna pitagórica primitiva. Sin embargo, la solución completa del problema no se obtuvo hasta el siglo XIII cuando Fibonacci encontró la forma de generar todas las ternas pitagóricas posibles.[3]
- Sólidos regulares. Los pitagóricos descubrieron el dodecaedro y demostraron que sólo existen 5 poliedros regulares.
- Números perfectos. Estudiaron los números perfectos,es decir aquellos números que son iguales a la suma de sus divisorespropios (por ejemplo 6=1+2+3). Encontraron una fórmula para obtenerciertos números perfectos pares.
- Números amigables. Un par de números son amigables si cada uno es igual a la suma de los divisores propios del otro. Jámblico atribuye a Pitágoras haber descubierto el par amigable (220, 284).
- Números irracionales. El descubrimiento de que la diagonalde un cuadrado de lado 1 no puede expresarse como un cociente denúmeros enteros marca el descubrimiento de los números irracionales.
- Medias. Los pitagóricos estudiaron la relación entre lasmedias aritmética, geométrica y armónica de dos números y obtuvieron larelación
.
- Números figurados. Un número es figurado (triangular,cuadrangular, pentagonal, hexagonal, etc) si tal número de guijarros sepueden acomodar formando el polígono correspondiente con lados 1,2,3,etc (ver figura).
- http://es.wikipedia.org/wiki/Pitagoras
Albert Einstein (
14 de marzo de
1879 -
18 de abril de
1955), nacido en
Alemania y nacionalizado en
Estados Unidos en el año
1940, es el
científico más conocido e importante del
siglo XX.
[1] En
1905, siendo un joven físico desconocido, empleado en la Oficina de Patentes de
Berna (
Suiza), publicó su
Teoría de la Relatividad Especial. En ella incorporó, en un marco teórico simple y con base en postulados físicos sencillos . En
1915[2] presentó la
Teoría General de la Relatividad, en la que reformuló por completo el concepto de gravedad. Una de las consecuencias fue el surgimiento del estudio científico del origen y evolución del
Universo por la rama de la física denominada
cosmología. Muy poco después, Einstein se convirtió en un icono popular de la ciencia alcanzando fama mundial, un privilegio al alcance de muy pocos científicos. Obtuvo el
Premio Nobel de Física en
1921 por su explicación del
efecto fotoeléctrico y sus numerosas contribuciones a la
física teórica .
....
http://es.wikipedia.org/wiki/Albert_Einstein
Georg Cantor (n. San Petersburgo, 3 de marzo de 1845, m. Halle, 6 de enero de 1918 ) fue un matemático alemán, inventor con Dedekind de la teoría de conjuntos, que es la base de las matemáticas modernas. Gracias a sus atrevidas investigaciones sobre los conjuntos infinitos fue el primero capaz de formalizar la noción de infinito bajo la forma de los números transfinitos (cardinales y ordinales).
La teoría de conjuntos es una división de las matemáticas que estudia los conjuntos. El primer estudio formal sobre el tema fue realizado por el matemático alemán Georg Cantor en el Siglo XIX y más tarde reformulada por Zermelo.
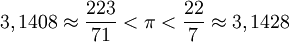
.png)
